ソーラーウォーマーの検討にあたって一番重要なのは直接日射がパネルに当たることです。

太陽エネルギーを熱に変換するものなので、天空光や間接光では運転しません。

しかし、実際の取り付けにあたっては設置可能場所が限られており、軒・ひさし下への取付や塀や手すりのある

バルコニーやベランダへの取り付けを検討される方もいらっしゃると思います。

 

 

 

 

今回は、設置計画マニュアルに沿って具体的にどのように設置場所を計画していくのか例を出しながら解説したいと思います。

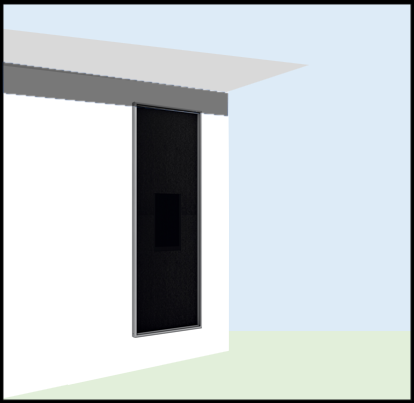
例えば、真南方向に下図イメージのようにひさしの下でソーラーウォーマーの壁付けを検討される場合。

 

 

 

先ずソーラーウォーマーにかかる日射の太陽高度を確認します。

太陽高度については以前、ブログ＆お知らせにて有料アプリをご紹介しましたが、

ke!sanー生活や実務に役立つ計算サイトーなどの無料サイトでも住所と観測時間の入力でだいたいの太陽高度を調べることもできます。

 

 

 

 

 

 

ちなみに例として弊社事務所住所で観測時刻を13時で入力すると、以下のように太陽高度が出ます。

	3月7日	6月20日（ほぼ夏至）	10月3日	12月22日（冬至）
太陽高度	45.97	69.25	45.27	27.93

太陽高度を調べる際は、日射時間の一番長い夏至と、逆に一番短い冬至、そしてその中間地点の春分・秋分の日（あるいはそれに近い日）の太陽高度を調べておくと、1年を通じてどのように日射が当たるのかをイメージしやすいです。

 

 

 

 

 

 

 

次に、この太陽高度を用いて軒・ひさしの影の長さを考えていきましょう。（高校数学の三角比の知識が必要となります。）

 

 

 

 

今回はざっくりわかればよいので、3月7日と10月3日の太陽高度はほぼ同じ45°と考えます。

すると軒・ひさしの影の部分が下図のように１：１：√2の直角二等辺三角形として

考えることができるので、庇の長さがそのまま影の長さ(=600)になることが分かります。

 

 

 

 

 

次に、6月２０日については太陽高度をおおよそ70°として考えます。

すると、壁側の三角形の鋭角は20°になるので、三角比を用いると

tan（20°）＝600/（壁にかかる影の長さ）　　となり、計算すると

（壁にかかる影の長さ）≒1704　となります。

 

 

 

 

 

最後に、12月24日については太陽高度をおおよそ28°として考えると、

壁側の角度は62°なので、

tan(62°）＝（壁にかかる影の長さ）/600　となり、計算して

（壁にかかる影の長さ）≒323　となります。

 

 

 

 

 

 

ですので、年間を通じてソーラーウォーマーへの影の当たり方は下記のように変化するイメージです。

　　　

　　　　　　3月7日　　　　　　　　　　　　　　　6月20日　　　　　　　　　　　　　　10月3日　　　　　　　　　　　　　　　12月22日

 

 

 

こうすることで、ソーラーウォーマーにどれだけの日射があたるのかを予測することができます。

今回の場合だと秋～冬・春にかけての日射に比べ、梅雨～夏にかけては日射が当たりづらいことが分かります。

そのため、夏の活用をメインに考えている場合は、設置場所を再検討する必要があります。

また、秋～冬にかけてもソーラーウォーマーに少し影がかかっているので、斜め設置などを検討することで、

さらなる日射量を期待できるかもしれません。

 

 

 

 

 

 

 

このような形で、どの時期をメインに活用したいのかを考え、メインで活用したい時期の太陽高度を

考慮した設置をすることにより、効率よくソーラーウォーマーを稼働させることができます。

今回は、軒・ひさしがあるパターンのみでの解説ですが、手すり・塀があるパターンについては、設置計画マニュアルで解説しております。

是非、ソーラーウォーマーご検討の際はご一読いただきますとご参考になると思います。